 |
Using the Microscope.
Basic Tutorial. Numerical Aperture. |
Part 6 of 9 Page 1 of 3 |
 |
Using the Microscope.
Basic Tutorial. Numerical Aperture. |
Part 6 of 9 Page 1 of 3 |

The resolving power 1. The absolute limit to resolution imposed by the wavelength of the light illuminating the specimen. No instrument which forms its image by wave interference can resolve detail which is smaller than about half the wavelength of the wave energy (light in the case of the microscope) being used to examine the specimen. This is as true of the accoustic and the (transmission) electron microscope as it is of the light microscope. 2. The Numerical Aperture (N.A.) of the objective in use. To explain this term, it is necessary to show why the amount of detail that can be seen with the microscope depends not only on wavelength, but on the angle over which the objective is capable of receiving light from the specimen. This is in turn dependent upon the refractive indices of the media in the light path. N.A. is the lens specification which takes these factors into account, and is effectively an index of the objective's ability to resolve fine detail. An explanation of N.A. must necessarily deal with the optical phenomenon of diffraction. The following account of image formation by a microscope objective is essentially a simplified version of the diffraction theory (minus the mathematics) put forward by Ernst Abbe in 1873. Consider a subject under a brightfield microscope which has a pattern of detail in which very small opaque objects are separated from one another by a distance equal to their own diameter. The diagram below represents the diffraction which occurs at a single narrow slit, and is used here to illustrate what happens when light passes through the space separating the opaque objects of the above example. Given the approximation that the wavefront of light arriving at this slit from a very distant point source is planar, Huyghens' 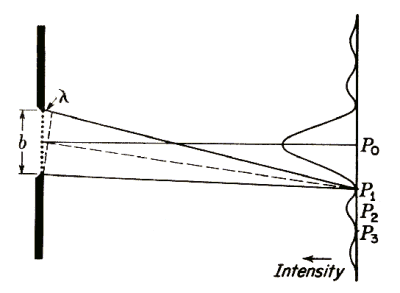
The point P1 on the screen is so situated that the light wavelet emanating from a point very close to the upper edge of the slit, and another emanating from a point very close to the lower edge of the slit have a path difference of one wavelength. Whilst these two rays interfere constructively, they are only two rays of the infinite number of ray pairs along the line b. To determine the net effect of the interaction of ray pairs across the entire aperture, consider the ray passing very close to the upper edge of the slit, and the ray immediately adjacent to and below it. Between these two rays, the path difference at P1 is extremely small, and the rays are very close to a condition of constructive interference -- but not quite. As second rays emanating from points further from the uppermost ray are considered, the path difference steadily increases until the ray from the centre of the slit is reached. With this ray, the path difference is half a wavelength, and total destructive interference occurs. A condition very close to total destructive interference also occurs with rays very close to the central ray. The degree of destructive interference gradually diminishes as second rays approaching the remote edge of the slit are selected and the interference is once more constructive. The result of this at the screen P is a zone of darkness on either side of the point P1, with P1 at the position of maximum darkness. Similarly, at the point P2, the path difference between the upper and lower rays is 1½ wavelengths, and P2 marks the centre of a zone of constructive interference -- called the first order diffraction maximum. And similarly on the other side of the axis. Second, third and higher order diffraction maxima are formed at points where the path difference is an odd number of half-wavelengths, and the intervening minima where the path difference is an even number of half-wavelengths. 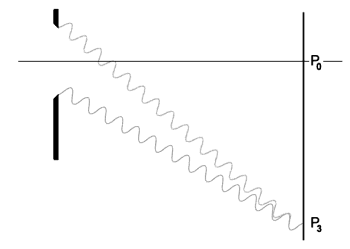 The diagram on the left shows the condition for the formation of the second order diffraction minimum (P3 above), where the path difference between the upper and lower rays is two wavelengths (four half wavelengths).
The diagram on the left shows the condition for the formation of the second order diffraction minimum (P3 above), where the path difference between the upper and lower rays is two wavelengths (four half wavelengths).
For an objective to form an image of the object detail represented by these diffracted rays, it must be capable of accepting them. As a minimum requirement, the objective must be capable of accepting both the axial rays (centred on P0) and at least part of the first-order diffraction maximum. The clarity with which any detail is rendered depends upon the percentage capture of the diffracted rays it generates. Complete capture of the first-order diffracted rays will produce an image which is capable of revealing detail close to the diffraction limit for that aperture. Second and third order maxima, being decreasingly intense, make less contribution to image detail. It should be clear from the diagram that the finer the detail in the specimen (the smaller the value of b), the greater the angle which must be assumed by the rays forming the various maxima in order to achieve the necessary path differences -- requiring the use of an objective of correspondingly larger angular aperture to capture them. Very fine detail will have maxima passing outside the aperture of the objective and will not be imaged. The ability of the objective to accept diffracted rays of a given angle is however strongly dependent on the refractive indices of the media between the objective and the specimen -- usually some combination of air, water, glass and oil. At this point the concept of Numerical Aperture becomes useful, and is dealt with in the next section. |